The science and technology world still uses a number of different measure systems, like the CGS system, mainly used in scientific publications, the technical system (or MKS), the British-American system, etc. The following tables show the base and derived units of measure of the International System (IS), together with the conversion factors of the most frequently used ones.
Units of Measure – International System (IS)
| Base units | Derived units | ||||
| Quantity | Unit | Symbol | Quantity | Unit | Symbol |
| Length | metre | m | Plane angle | radian | Rad |
| Mass | kilogram | kg | Solid angle | steradian | Sr |
| Time | second | s | |||
| Electric current | ampere | A | Notes: | ||
| Temperature | Kelvin | K | centigrades [°C] = degrees [K] – 273.15 | ||
| Luminous intensity | Candela | Cd | Degrees Fahrenheit [°F] = + 32 | ||
| Amount of substance | Mole | Mol | |||
Most frequently used IS derived units of measure
| Quantity | Unit | Symbol | Formula |
| Frequency (of a periodical event) | hertz | Hz | 1/s |
| Force | newton | N | (kg×m)/s2 |
| Pressure | pascal | Pa | N/m2 |
| Energy, work, quantity of heat | joule | J | N×m |
| Power | watt | W | J/s |
| Quantity of electricity, electric charge | coulomb | C | A×s |
| Electric potential, electromotive force, potential difference | volt | V | W/A |
| Capacitance | farad | F | C/V |
| Electric resistance | ohm | W | V/A |
| Conductance | siemens | S | A/V |
| Magnetic flux | weber | Wb | V×s |
| Magnetic flux density | tesla | T | Wb/m2 |
| Inductance | henry | H | Wb/A |
| Luminous flux | lumen | Lm | cd×sr |
| Illuminance | lux | Lx | lm/m2 |
| Activity (of radioactive substances) | becquerel | Bq | 1/s |
| Absorbed dose | gray | Gy | J/kg |
Note: 1 calorie = 4.184 joule
Prefixes used in the IS
| Multiplying factor (= scientific note) | Prefix | Symbol | |
| 1 000 000 000 000 000 000 000 000 | = 1024 | Yotta | Y |
| 1 000 000 000 000 000 000 000 | = 1021 | Zetta | Z |
| 1 000 000 000 000 000 000 | = 1018 | Exa | E |
| 1 000 000 000 000 000 | = 1015 | Peta | P |
| 1 000 000 000 000 | = 1012 | Tera | T |
| 1 000 000 000 | = 109 | Giga | G |
| 1 000 000 | = 106 | Mega | M |
| 1 000 | = 103 | Kilo | K |
| 100 | = 102 | Hecto | H |
| 10 | = 101 | Deka | Da |
| 0.1 | = 10-1 | Deci | D |
| 0.01 | = 10-2 | Centi | C |
| 0.001 | = 10-3 | Milli | M |
| 0.000 001 | = 10-6 | Micro | m |
| 0.000 000 001 | = 10-9 | Nano | N |
| 0.000 000 000 001 | = 10-12 | Pico | P |
| 0.000 000 000 000 001 | = 10-15 | Femto | F |
| 0.000 000 000 000 000 001 | = 10-18 | Atto | A |
| 0.000 000 000 000 000 000 001 | = 10-21 | Zepto | Z |
| 0.000 000 000 000 000 000 000 001 | = 10-24 | Yocto | Y |
The 11th Conférence Générale des Poids et Mésures (CGPM) in 1960 adopted the first series of prefixes and symbols for the decimal multiples and submultiples of the International System units.
The 10-15 and 10-18 prefixes were introduced in 1964 by the 12th CGPM.
The 1015 and 1018 prefixes were introduced in 1975 by the 15th CGPM.The 1021, 1024, 10-21 and 10-24 prefixes, proposed in 1990 by the CIPM, were approved in 1991 by the 19th CGPM.
Rules of writing for the IS units of measure
The IS has laid down the rules for writing names and symbols of physical quantities. We report herebelow the most important ones:
- Units names must always be written in lower-case characters, with no accent or other graphical notations.
Example: ampere, not Ampère.
- Units names have no plural.
Example: 3 ampere, not 3 amperes.
- Units symbols must be written with a lower-case initial, except for those deriving from people’s names.
Example: mol for mole, K for Kelvin.
- The symbols must not be followed by dots (except when at period end).
- Symbols must always come after the numerical values.
Example: 1 kg , not kg 1.
- The product of one or more units is indicated by a dot halfway up or small space between their symbols.
Example: N·m or N m.
- The ratio between two units is indicated with a slash or negative index.
Example.: J/s or J×s-1).
Units of measure – definition
We give herebelow the definitions for the units of measure of a few base quantities.For each unit is indicated the Conférence Générale des Poids et Mésures (GCPM) that introduced it.
Time
Second is the duration of 9 192 631 770 periods of the radiation emitted bya Caesium 133 atom during the transition between the hyperfine (F=4, M=0) and (F=3, M=0) levels of its 2S(1/2) fundamental state.
(13th GCPM, 1967)
The primary reference sample is a caesium clock. A caesium clock can make a maximum relative error of 1×10-12, equivalent to 1 ms every 12 days.
Length
Metre is the distance covered by lightin a vacuum during a time interval equal to 1/299 792 458 of a second.
(17th CGPM, 1983)
The propagation speed of electromagnetic waves in a vacuum (speed of light) is one of physics fundamental constants. Following the definition of metre introduced in 1983, its value is taken to be an exact and non modifiable value:
299 792 458 m/s.
The recommended way to make a metre reference sample is to use the monochromatic radiation emitted by a helium-neon laser in the visible red region (633 nm wavelength).
Mass
Kilogram is the international prototype mass kept at the Pavillon de Breteuil (Sevres, France).
(3rd CGPM, 1901)
It is the only IS base unit represented by an artificial sample. This is a platinum-iridium cylinder, 38 mm in diameter and height, kept under a triple glass case, in a vacuum, together with 6 other control samples, in the conditions set up bythe 1st CGPM in 1889.
The sample relative precision is in the order of 10-9.
The introduction of natural mass sample based on atomic properties is currently under study.
Temperature
Kelvin is 1/273.16 of the thermodynamic temperature of water’s triple point.
(13th CGPM, 1967)
A substance triple point is the thermodynamic state where the three phases (liquid, solid and gas are at equilibrium). Water’s triple point occurs at a pressure of 610 Pa and (by definition) a temperature of 273.16 K, corresponding to 0.01 °C.
The precision in measuring the temperature of water’s triple point is c. 1×10-6.
Quantity of a substance
Mole is the quantity of a substance containing as many elementary entities as the atoms contained in 0.012 kg carbon 12. When using the mole as unit of measure, we must specify the nature of the elementary entities, which can be atoms, molecules, ions, electrons, other particles or specific groups of such particles.
(14th CGPM, 1971)
(17th CGPM, 1983)
12C (carbon 12) is the most abundant carbon isotope: its atomic nucleus is made up of 6 protons and 6 neutrons.
When we use the mole as unit of measure we must specify the nature of the elementary entities we are referring to: number of moles of atoms, molecules, ions, etc.
The number of elementary entities making up 1 mole is called Avogadro number; its approximate value is
NA= 6.022×1023.
Electric current intensity
One ampere is the current that, flowing in two parallel, indefinitely long conductors (the cross-section value is irrelevant) placed at 1 metre distance from each other in a vacuum, produces a force equal to 2×10-7 newton per metre length.
(9th CGPM, 1948)
We define the ampere by referring to the law describing the interaction force F between two parallel conductors of length s and distance d, carrying respectively current I1 and I2: F = 2 km×I1×I2×s/d, where the km constant is assigned the value 10-7 (in general, km is expressed as a function of the magnetic permeability in a vacuum m0: km = m0/4p).
According to the IS definition, ampere values can be obtained with an electrodynamometer, an instrument measuring the force between two conductors run through by a current. The common practice, however, is to refer to Ohm’s law (I=V/R) and obtain the current (I expressed in ampère) as the ratio between potential difference (V expressed in volts) and resistance (R expressed in ohm). The reference sample for potential difference (volt) and resistance (ohm) are currently obtained by referring to two quantum phenomena, the Josephson and Hall quantum effect respectively.
Light intensity
Candela is the light intensity, in one assigned direction, of a source emitting a monochromatic radiation with frequency 540×1012 Hz and whose energy intensity in such direction is 1/683 W/sr.
(16th GCPM, 1979)
Photometry measures the properties of electromagnetic radiations in the range perceived by the human eye (the so called visible light). The average human eye is sensitive to electromagnetic radiations in a wavelength range of 400nm – 750nm (corresponding respectively to violet and red). Maximum sensitivity is registered for a wavelength of about 556 nm, corresponding to a frequency of 540×1012 Hz.
Light intensity is photometry main quantity; it corresponds to the energy emitted by a light source in the time unit and solid angle unit, weighed according to the human eye average sensitivity curve.
Conversion tables for units of measure most commonly used in technical calculations
| Unit | cm | m (*) | In | ft | |
|---|---|---|---|---|---|
|
1 cm
|
=
|
1
|
0.01
|
0.3937
|
0.032808
|
|
1 m (*)
|
=
|
100
|
1
|
39.37
|
3.28083
|
|
1 in
|
=
|
2.540
|
0.0254
|
1
|
0.08333
|
|
1 ft
|
=
|
30.480
|
0.3048
|
12
|
1
|
(1) In this and the following tables, International System units are indicated in (*).
Note:
in = inches
ft = feet
Example
To convert length values from inches to centimetres, just multiply the inch values by the conversion factor seen in the box where the row containing the starting unit of measure (in this case inches) meets the column containing the final unit of measure (in this case centimetres):
2.5 in = 2.5×2.540 cm = 6.35 cm
| Units | cm2 | M2 (*) | sq.in (= in2) | sq.ft (= ft2) | |
|---|---|---|---|---|---|
|
1 cm2
|
=
|
1
|
10-4
|
0.155
|
1.0764×10-3
|
|
1 m2 (*)
|
=
|
104
|
1
|
1550
|
10.764
|
|
1 sq.in (= 1 in2)
|
=
|
6.4516
|
6.4516×10-4
|
1
|
6.944×10-3
|
|
1 sq.ft (= 1 ft2)
|
=
|
929.034
|
0.0929
|
144
|
1
|
| Units | g | Kg (*) | Lb | |
|---|---|---|---|---|
|
1 g
|
=
|
1
|
10-3
|
2.2046×10-3
|
|
1 kg (*)
|
=
|
103
|
1
|
2.2046
|
|
1 lb
|
=
|
453.59
|
0.45359
|
1
|
Note: lb = pounds
| Units | cm3 | litre | cubic in (= in3) | cubic ft (= ft3) | Gal | m3 (*) | |
|---|---|---|---|---|---|---|---|
|
1 cm3
|
=
|
1
|
0.99997×10-3
|
0.061023
|
3.5314×10-5
|
2.6417×10-4
|
10-6
|
|
1 litre
|
=
|
1000.028
|
1
|
61.025
|
0.0353
|
0.264
|
10-3
|
|
1 cubic in (= in3)
|
=
|
16.387
|
1.63867×10-2
|
1
|
5.7870×10-4
|
4.3290×10-3
|
1.639×10-5
|
|
1 cubic ft (= ft3)
|
=
|
28317.017
|
28.316
|
1728
|
1
|
7.4805
|
0.0283
|
|
1 US gal
|
=
|
3785.4345
|
3.7853
|
231.0000
|
0.13368
|
1
|
3.785×10-5
|
|
1 m3 (*)
|
=
|
104
|
999.97
|
6.1×104
|
35.315
|
264.18
|
1
|
Definition: 1 litre is defined as the volume occupied by 1 kg water at 4°C temperature and 760 torr pressure. It exceeds by about 28 mm3 the volume of 1 dm3; therefore:
1 litre » 1 dm3 = 1000 cm3 (cc)
1 ml (millilitre) » 1 cm3
Note:
US gal = United States gallon
UK gal = United Kingdom gallon
1 UK gal = 4.5460 litres
Force units:
- Newton (N) is the force required to impart an acceleration of 1 m/s2 to a 1 kg mass body;
thus N = kg×m/s2.
- Kilogram (weight) or kilogram (force) (kgw or kgf) is the force required to impart the acceleration of 1 g to a 1 kg mass body;
- Dyne is the force required to impart the acceleration of 1 cm/s2 to a 1 g mass body;
thus dyne = ×cm/s2 Note: 1 kgp » 9.8067 N 1 N = 105 dyne psi = pounds per squared inches
| Unit | g/cm3 = kg/litre | Kg/m3 = g/litre (*) | lb/cubic ft | |
|---|---|---|---|---|
| 1 g/cm3 = 1 kg/litre | = | 1 | 1000 | 62.6 |
| 1 kg/m3 = 1 g/litre (*) | = | 0.001 | 1 | 0.0625 |
| 1 lb/cubic ft | = | 0.016 | 16 | 1 |
| Unit | Poise | CP | lb/(ft×h) | N×s/m2 (*)= Pa×s | |
|---|---|---|---|---|---|
|
1 Poise =
= 1 g/(cm×s) = 1 dyne×s/cm2
|
=
|
1
|
100
|
242
|
0.1
|
|
1 cP
|
=
|
0.01
|
1
|
2.42
|
10-3
|
|
1 lb/(ft×h)
|
=
|
0.00413
|
0.413
|
1
|
4.13×10-4
|
|
1 N×s/m2 (*)= Pa×s
|
=
|
10
|
103
|
2.42×103
|
1
|
Note:
1 mPa×s = 1 Poise (cP)
Definition: kinematic viscosity (n) º ratio between viscosity (m) and density (r) of the fluid at hand; thus n = m/r .
IS Unit of measure: m²/s
CGS Unit of measure: stoke (St), equal to cm²/s
Example of conversion between different units of measure
Let’s suppose we want to convert a compression strength value from MPa to kgp/cm²; what is the conversion factor?
1 MPa = 106 Pa = 106(N/m²)
We must now convert N into kgp and m² into cm²
=
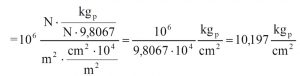
=
The conversion factor from MPa to kgp/cm² is 10.2. The conversion factor between Pa and kgp/cm² quoted on the “Pressure Units” table is 1.02×10-5; multiplying it by 106 (to go from Pa to MPa) we obtain the same result.




